5-两阶段最小二乘法

5-两阶段最小二乘法

比如我们想要研究教育程度（接受教育年份，暴露因素X）对未来收入（薪资，结局变量Y）的影响。

这里我使用ivreg 中的数据集：

data("SchoolingReturns", package = "ivreg")
my_data <- SchoolingReturns[, 1:8]

Rows: 3,010
Columns: 8
$ wage        <dbl> 548, 481, 721, 250, 729, 500, 565, 608…
$ education   <dbl> 7, 12, 12, 11, 12, 12, 18, 14, 12, 12,…
$ experience  <dbl> 16, 9, 16, 10, 16, 8, 9, 9, 10, 11, 13…
$ ethnicity   <fct> afam, other, other, other, other, othe…
$ smsa        <fct> yes, yes, yes, yes, yes, yes, yes, yes…
$ south       <fct> no, no, no, no, no, no, no, no, no, no…
$ age         <dbl> 29, 27, 34, 27, 34, 26, 33, 29, 28, 29…
$ nearcollege <fct> no, no, no, yes, yes, yes, yes, yes, y…

代码部分简单带过，这里主要以原理介绍为主。

我们首先发现教育程度与未来收入确实是显著相关的p-value: < 2.2e-16。

> summary(lm(formula = wage ~ education, data = my_data))

Call:
lm(formula = wage ~ education, data = my_data)

Residuals:
    Min      1Q  Median      3Q     Max 
-576.09 -173.36  -34.12  127.82 1686.25 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept)  183.949     23.104   7.962 2.38e-15 ***
education     29.655      1.708  17.368  < 2e-16 ***
---
Signif. codes:  
0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 250.7 on 3008 degrees of freedom
Multiple R-squared:  0.09114,	Adjusted R-squared:  0.09084 
F-statistic: 301.6 on 1 and 3008 DF,  p-value: < 2.2e-16

接下来，我们就要使用两阶段最小二乘估计，来定量估计暴露因素X与Y之间的关联效应大小。

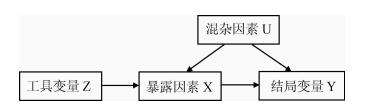
两阶段最小二乘估计分为两个阶段，第一阶段是将自变量的变异分解，使用工具变量对暴露因素建立回归；第二步再通过暴露因素预测值（predicted value，P）构建和结局变量Y之间的回归方程。

比如说这里我们发现有一个变量，即距离学校距离是否近。我们发现，与学校距离远近，不仅与教育程度（接受教育年份，暴露因素X）相关，它同样与未来收入（薪资，结局变量Y）相关。那么，这里学校距离远近就是一个潜在的工具变量。

5.1-第一阶段

我们首先需要明确工具变量对暴露因素的作用。

这里首先需要构建Z-X 回归模型：X = α + dZ + ε。除了要看工具变量以外，还要加上外生变量做回归。

这里主要有两个目的：

• 明确工具变量对自变量的作用，看该变量与我们的自变量（暴露因素）之间是否是高度相关的；

• 获得暴露因素预测值，以作为第二阶段的自变量。

5.2-第二阶段

第二阶段就是用工具变量对自变量的预测值来估计回归系数：Y=α + βX(Z对X的预测值) +ε

因此这个式子实际可以合并为Y = α + dZ + ε

即：